الدوال المثلثية في المثلثات القائمة الزاوية

الدوال المثلثية في المثلثات القائمة الزاوية  هناك العديد من الدوال المثلثية في المثلثات القائمة الزاوية ، ومعرفة الدوال المثلثية في المثلثات القائمة الزاوية لها أهمية كبيرة في الحسابات الرياضية ، وتساعد في إيجاد جميع المتغيرات غير المعروفة في أي مسألة رياضية ، بناءً على عدة خطوات متبعة الوصول إلى المتغير المراد إيجاده.
موقع الماميز يضع هذا الموضوع بين أيديكم .

---

المثلث قائم الزاوية

المثلث القائم الزاوية يشبه المثلثات الأخرى من حيث احتوائه على ثلاثة جوانب ، لكن طول الضلع الأكبر فيه يسمى الوتر ، بالإضافة إلى أنه يشبه المثلثات الأخرى حيث يجب أن يكون مجموع زواياه يساوي 180 درجة ، لكن أهم ما يميزها هو أن إحدى الزوايا يجب أن تكون 90 درجة ، لاحظ أيضًا أن الوتر يجب أن يكون مقابل الزاوية 90.

الدوال المثلثية في المثلثات القائمة الزاوية

تكمن أهمية معرفة الدوال المثلثية في إمكانية استخدامها لإيجاد أطوال الأضلاع المفقودة في المثلثات القائمة الزاوية ، وكذلك الزوايا الناقصة.

بادئ ذي بدء ، وقبل التعرف على الدوال المثلثية في المثلثات القائمة الزاوية ، يجب أن نتذكر نظرية فيثاغورس للمثلثات القائمة الزاوية ، والتي من خلالها يمكننا إيجاد طول أي ضلع غير معروف ، ومعادلة هذه النظرية هي كما يلي يتبع:

الوتر ^ 2 = الضلع الأول ^ 2 + الضلع اثنان ^ 2

وإذا أعطيت أي زاوية ، فيجب تحديد الضلع المقابل والجانب المجاور لها ، بالإضافة إلى الوتر ، لأن تحديد هذه الجوانب هو الذي سيساعدنا في تحديد الدوال المثلثية ، ومن بين الدوال المثلثية في اليمين – المثلثات المتشابكة ، والمقبولة هي كالتالي:

شرط

الوظيفة الأولى في المثلث القائم الزاوية هي الجيب ، والمختصرة بالجيب θ
حيث θ = طول الضلع المقابل٪ طول الوتر

جيب التمام

يُشار إلى جيب التمام لزاوية بالرمز cosθ
حيث cos θ = طول الضلع المجاور٪ الوتر

ظل

يتم الإشارة إلى الظل بالرمز θ
حيث θ = طول الضلع المقابل٪ من طول الضلع المجاور

قاطع الزاوية

حيث يتم الإشارة إلى الزاوية القاطعة بالرمز θ
حيث θ = طول الوتر٪ طول الضلع المقابل

قاطع من جميع الزوايا

يُشار إلى قاطع التمام بالرمز θ
حيث θ = طول الوتر٪ طول الضلع المجاور

ظل الزاوية الكاملة

يُرمز إلى ظل الزاوية ب cotan θ
حيث cot θ = طول الضلع المجاور٪ طول الضلع المقابل

إقرأ أيضا :ما معنى خصخصة التعليم؟ أهداف ومزايا خصخصة التعليم

---

أمثلة على الدوال المثلثية في المثلثات القائمة الزاوية

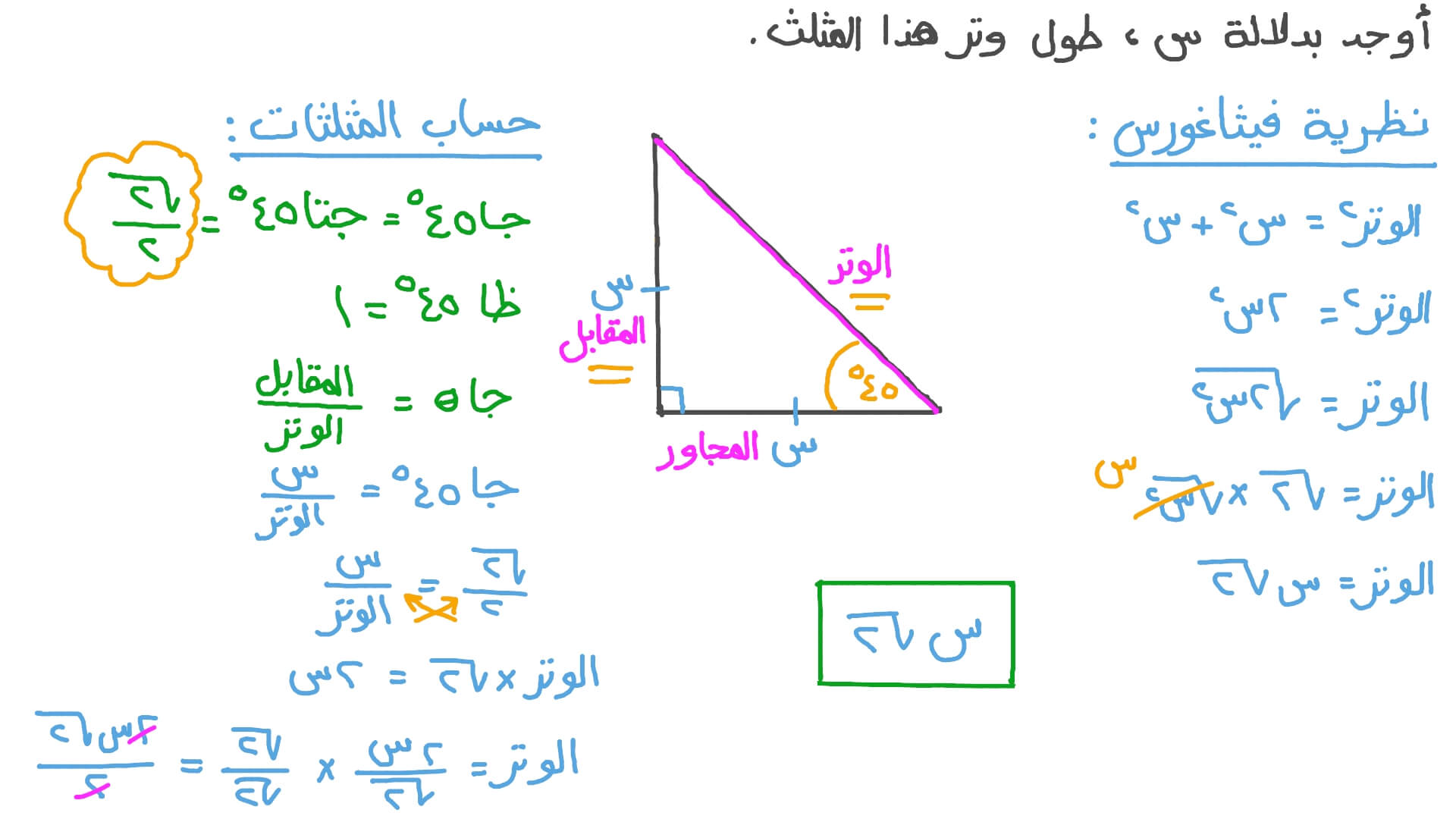
هناك العديد من الأسئلة حول الدوال المثلثية في المثلثات القائمة الزاوية ، بناءً على البيانات الواردة في أي سؤال. ومنهم من يعرف أطوال الأضلاع ، وإحدى قياسات الزوايا غير معروفة ، وبعضها مذكور في السؤال إحدى الزوايا ، وإما واحد أو اثنان من أطوال الأضلاع غير معروف. ، ويجب العثور عليها.

إيجاد الزاوية بناءً على معلومات حول أطوال ضلعين على الأقل في مثلث قائم الزاوية

مثال: أوجد قياس الزاوية في مثلث قائم الزاوية طوله 25 سم وطول الضلع المقابل للزاوية المفقودة 12 سم.

الحل: بما أننا نعرف طول الوتر وطول الضلع المقابل للزاوية ، فإننا نستخدم قانون الجيب.

sin θ = المقابل٪ الوتر
كاθ =
12/25 = 0.48

لإيجاد الزاوية باستخدام الآلة الحاسبة ، نضغط على زر shift ونضع الرقم 0.48 ، إذن الإجابة هي 29º ، وهو قياس الزاوية المطلوب.

إقرأ أيضا :تعليم جدول الضرب للأطفال بطريقة سهلة

---

حساب طول أحد الأضلاع ، بمعلومية قيمة إحدى الزوايا وقيمة أحد الأضلاع

مثال 1: سلم طوله 30 سم يتكئ على جدار ، والزاوية بين السلم والأرض 32 درجة. ما هو ارتفاع المبنى الذي يصل منه السلم؟

الحل: أولاً ، باستخدام الآلة الحاسبة ، نجد جيب الزاوية 32 ، لأنه يساوي 0.5299 ، ونعوض به في القانون التالي

sinθ = طول الضلع المقابل٪ من الوتر
0.5299 = طول الضلع المقابل 30٪.
بحل هذه المعادلة ، فإن الارتفاع الذي سيصل إليه السلم يساوي 15.9 سم.

مثال 2: لديك مثلث قائم الزاوية ، إحدى زواياه موضوعة على خط يساوي 45 سم يساوي 62 ، فأوجد طول الضلع المقابل للزاوية.

الحل: بما أن المعلومات المعطاة هي زاوية ، وطول الضلع المجاور ، فإن الحل يعتمد على قانون الظل ، على النحو التالي:

tan θ = طول الضلع المقابل٪ طول الضلع المجاور
ونجد من الآلة الحاسبة ظل الزاوية 62 ، والإجابة ستكون 1.0887 وبالتعويض في القانون
1.0887 = طول الضلع المقابل 45٪.
إذن ، طول الضلع المقابل 84.6 سم.

في نهاية هذا المقال ، نلخص أهم النتائج ، وهي أن الدوال المثلثية في المثلثات القائمة الزاوية (Right triangle)  هي الجيب وجيب التمام والظل ، بالإضافة إلى توضيحها من خلال حل أمثلة متعددة.

إقرأ أيضا :مميزات وعيوب الذكاء الاصطناعي